フェルマーの最終定理
サイモン・シン著 青木 薫訳 新潮社 2000.1.30初版刊 00/8/9

 「私はこの命題の真に驚くべき証明を持っているが、余白が狭すぎるのでここに記すことは出来ない」。
「私はこの命題の真に驚くべき証明を持っているが、余白が狭すぎるのでここに記すことは出来ない」。
17世紀にフェルマーが残した超難問を、数学者ワイルズが1995年に完全証明した。ピュタゴラスに始まる数論、
解決の鍵となった『谷山=志村予想』など、数学をめぐる「歴史ドラマ」を分かりやすく感動的に描いた傑作。
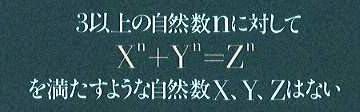
 ワイルズの証明は非常に高度な数学が使われているけれども、フェルマーの最終定理の美しさは、問題そのものを
理解するのは簡単だという点にある。それは小学生でもわかるように述べられたパズルなのだ。
ワイルズの証明は非常に高度な数学が使われているけれども、フェルマーの最終定理の美しさは、問題そのものを
理解するのは簡単だという点にある。それは小学生でもわかるように述べられたパズルなのだ。
ルネッサンスの伝統に生きたピエール・ド・フェルマーは、古代ギリシャの知識を再発見するという活動の真っ只中にあった。
だが、彼はギリシャ人が問わなかった問題を問いかけ、それによって世界一の難問を生んだのである。フェルマーが残した
思わせぶりなメモによれば、彼自身はその答えを知っているという。
だが、答えそのものは記されていなかった。3世紀に
及ぶ探求劇の幕が切って落とされた。
 数学は、人間の思考の中でも、もっとも純粋なものの一つであり、数学者という人たちは、門外漢の目には別世界の住人の
ように見える。数学者と話をしていて驚かされるのは、彼らの話す内容の恐ろしく正確なことだった。質問をしても即座に
返事が返ってくることはなく、彼らの頭の中で答えの構造が完全に出来上がるまで待たされることもしばしばだった。
数学は、人間の思考の中でも、もっとも純粋なものの一つであり、数学者という人たちは、門外漢の目には別世界の住人の
ように見える。数学者と話をしていて驚かされるのは、彼らの話す内容の恐ろしく正確なことだった。質問をしても即座に
返事が返ってくることはなく、彼らの頭の中で答えの構造が完全に出来上がるまで待たされることもしばしばだった。
だが、彼らがいったん口を開けば、明晰で考え抜かれた、これ以上望めないほどの答えをくれるのだ。ワイルズの友人である
ピーター・サーナクにこの点について尋ねたところ、数学者はただ、間違ったことを口にするのがいやなだけだと話してくれた。
もちろん、数学者も直感やインスピレーションを利用するけれども、改まった発言は完全無欠でなければならないのだ。
数学の核心は証明にある。そして証明こそは、数学と科学の他の分野とをきっぱり分かつものなのだ。
数学以外の科学分野ではまず仮説を立て、実験によってそれを検証する。そして仮説の誤りが示されれば、別の仮説がそれにとって代わる。
しかし数学においては、完全な証明こそがゴールである。一度証明されるということは、永久に証明されることなのだ。そこに変更の
余地はない。
フェルマーの最終定理の場合も、証明こそが数学者の挑むべき難関であり、証明を発見した者が、数学界全体の賞賛を受ける
ことになる。
 数学上の驚くべき工夫と、真の閃きとによって、アンドリューはついにフェルマーの問題に終止符を打ったのである。
数学上の驚くべき工夫と、真の閃きとによって、アンドリューはついにフェルマーの問題に終止符を打ったのである。
アンドリュー自身の口から、7年間の孤独な研究や、それに続いた地獄のような1年間の話を聞いた。アンドリューはこれまで
誰にも語ったことのない、心の奥底に秘めた思いを聞かせてくれた。30年もの間子供時代の夢を手放さずにいられたのはなぜか、
そうとは知らずに研究していた数学が、結局はフェルマー問題を攻略するための道具になってくれたこと、いつもそばにあった
フェルマー問題がなくなった喪失感、そして開放感からくる精神の高揚・・・・・
 アンドリュー・ワイルズの探求の旅は、次のような章立てで語られている。
アンドリュー・ワイルズの探求の旅は、次のような章立てで語られている。
第1章 「ここで終わりにしたいと思います」
第2章 謎をかける人
第3章 数学の恥じ
第4章 抽象の中へ
第5章 背理法
第6章 秘密の計算
第7章 小さな問題点
第8章 数学の大統一

 「私はこの命題の真に驚くべき証明を持っているが、余白が狭すぎるのでここに記すことは出来ない」。
「私はこの命題の真に驚くべき証明を持っているが、余白が狭すぎるのでここに記すことは出来ない」。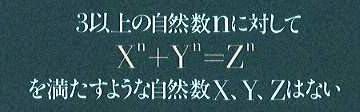
 ワイルズの証明は非常に高度な数学が使われているけれども、フェルマーの最終定理の美しさは、問題そのものを
理解するのは簡単だという点にある。それは小学生でもわかるように述べられたパズルなのだ。
ワイルズの証明は非常に高度な数学が使われているけれども、フェルマーの最終定理の美しさは、問題そのものを
理解するのは簡単だという点にある。それは小学生でもわかるように述べられたパズルなのだ。 数学は、人間の思考の中でも、もっとも純粋なものの一つであり、数学者という人たちは、門外漢の目には別世界の住人の
ように見える。数学者と話をしていて驚かされるのは、彼らの話す内容の恐ろしく正確なことだった。質問をしても即座に
返事が返ってくることはなく、彼らの頭の中で答えの構造が完全に出来上がるまで待たされることもしばしばだった。
数学は、人間の思考の中でも、もっとも純粋なものの一つであり、数学者という人たちは、門外漢の目には別世界の住人の
ように見える。数学者と話をしていて驚かされるのは、彼らの話す内容の恐ろしく正確なことだった。質問をしても即座に
返事が返ってくることはなく、彼らの頭の中で答えの構造が完全に出来上がるまで待たされることもしばしばだった。 数学上の驚くべき工夫と、真の閃きとによって、アンドリューはついにフェルマーの問題に終止符を打ったのである。
数学上の驚くべき工夫と、真の閃きとによって、アンドリューはついにフェルマーの問題に終止符を打ったのである。 アンドリュー・ワイルズの探求の旅は、次のような章立てで語られている。
アンドリュー・ワイルズの探求の旅は、次のような章立てで語られている。